TAREA MATLAB
Contents
Ejercicio1
Funcion recursiva para calcular factorial de un numero
type factr
function f = factr(n)
if n == 0
f = 1;
else
f = n * factr(n-1);
end
Función combina que devuelve el número de combinaciones de tamaño i de una colección de tamaño n, que usa la función factorial recusivo
type combina
function t = combina(n,i)
t=(factr(n))/((factr(i))*(factr(n-i)));
end
Desarrollar una función de nombre bernstein que devuelva el valor del polinomio de Bernstein
type bernstein
function b=bernstein(n,i,t);
b=combina(n,i).*t.^i.*(1-t).^(n-i);
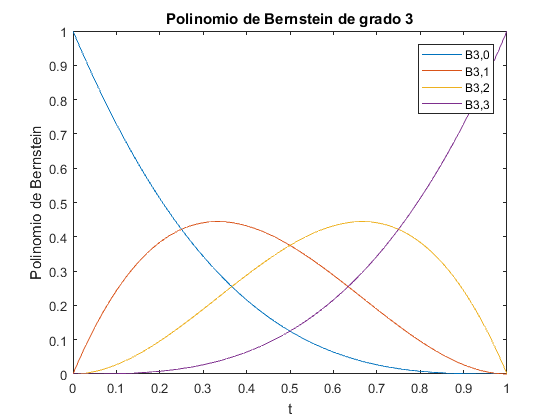
Desarrollar una función que use la función bernstein y vectorización para dibujar en la misma gráfica los polinomios de bernstein de grado 3.
t=linspace(0,1);
n=3;
for i=0:n
b=bernstein(n,i,t);
figure(1)
plot(t,b)
hold on;
end
xlabel('t');
ylabel('Polinomio de Bernstein');
title('Polinomio de Bernstein de grado 3');
legend('B3,0','B3,1','B3,2','B3,3');
hold off
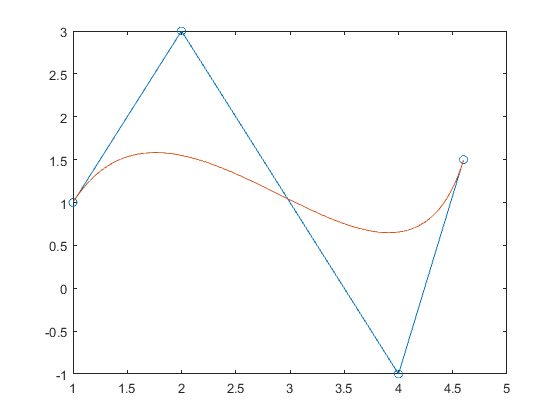
Desarrollar un programa para graficar el polígono de control y la curva de Bézier
t=linspace(0,1);
V=[1 2 4 4.6;1 3 -1 1.5];
plot(V(1,:),V(2,:),'-o')
n=size(V);
n=n(2);
s=size(t);
x=zeros(n,s(2));
y=zeros(n,s(2));
for i=1:n
x(i,:)=bernstein(n-1,i-1,t)*V(1,i);
y(i,:)=bernstein(n-1,i-1,t)*V(2,i);
end
a=sum(x);
b=sum(y);
hold on;
plot(a,b);
Ejercicio 2
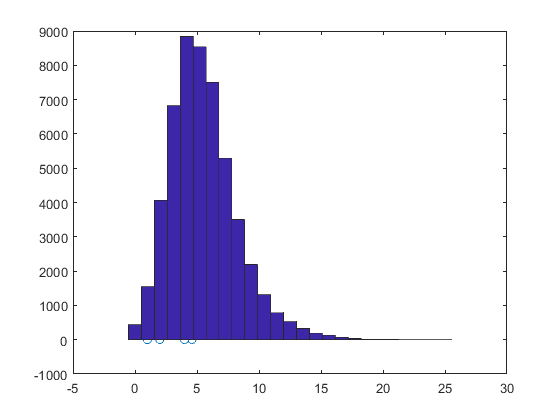
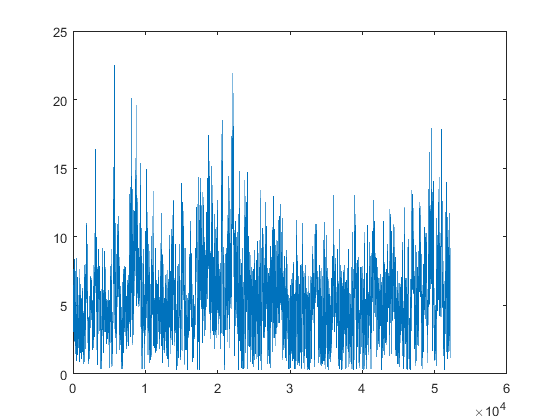
Script que lea los datos de velocidad del viento (xlsread) y grafique el histograma (hist) considerando intervalos de clase entre [0,25]
dw=xlsread('sotaventogaliciaanual.xlsx');
nbins=linspace(0,25,25);
figure(1)
hist(dw,nbins)
figure(2)
plot(dw)
clear,clc
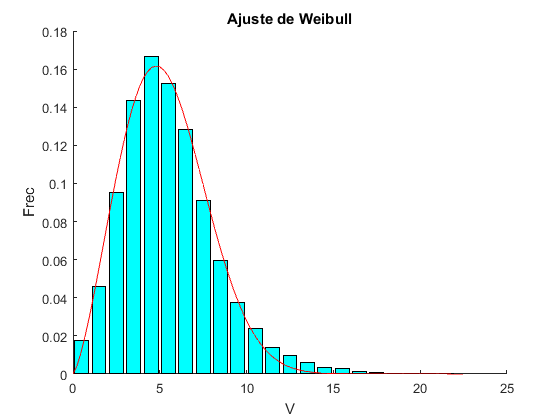
Script que lea los datos de velocidad del viento (xlsread), los convierta a un histograma de frecuencias y ajuste a una distribución de Weibull mediante una regresión no lineal (nlinfit) usando como valores iniciales de los parámetros k y c los valores del promedio y el cuadrado de la desviación estándar de la velocidad del viento respectivamente. Graficar en un mismo gráfico el diagrama de frecuencias y la curva de ajuste
Y=xlsread('sotaventogaliciaanual.xlsx','B:B');
x=0.5:1:max(Y);
viento=hist(Y,x);
frec=viento/sum(viento);
f=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
k=std(Y);
c=mean(Y);
a0=[k c];
af=nlinfit(x,frec,f,a0);
figure(3)
hold on
bar(x,frec,'c');
x=linspace(0,max(Y),100);
y=f(af,x);
plot(x,y,'r')
title('Ajuste de Weibull')
xlabel('V')
ylabel('Frec')
hold off
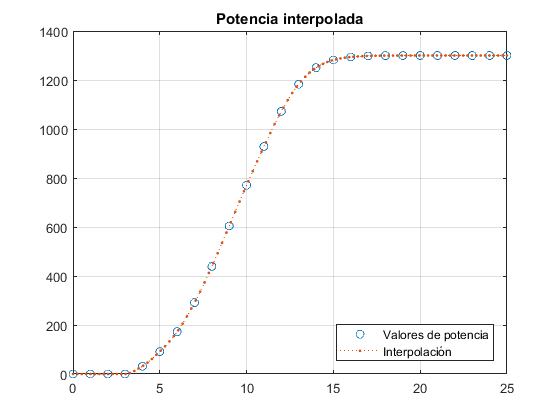
Desarrollar un script para interpolar (interp1) la curva de potencia del generador mediante un polinomio cúbico (pchip). Graficar los puntos de la curva y los valores de la interpolación.
X=xlsread('sotavento_curva potencia.xlsx','A:A');
Y=xlsread('sotavento_curva potencia.xlsx','B:B');
figure(4)
x25=linspace(0,25);
v25 = interp1(X,Y,x25,'pchip');
plot(X,Y,'o',x25,v25,':.');
title('Potencia interpolada')
legend('Valores de potencia','Interpolación','Location','southeast');
grid on
hold off
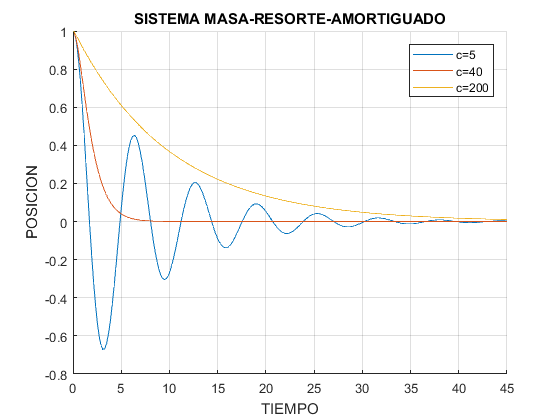
Ejercicio 3
figure(8)
clear all, clc
m=20;
k=20;
c=[5 40 200];
x0=[1,0];
tf=45;
hold on
for i=1:3
f=@(t,x) [x(2);(-c(i)*x(2)-k*x(1))/m];
[t,x]=ode45(f,[0,tf],x0);
plot(t,x(:,1))
end
grid on
xlabel('TIEMPO')
ylabel('POSICION');
legend('c=5','c=40','c=200')
title('SISTEMA MASA-RESORTE-AMORTIGUADO')
Ejercicio 4